DFS and BFS

These acronyms, of course, refer to depth first search and breadth first search. These are two different high-level algorithms for traversing a tree data structure.

In these examples, let’s consider a binary tree in which each node is an integer, and we want to search for a node in the tree with a certain integer value.

Depth First Search

Depth first search works by starting from the root node, then following a branch until it reaches a leaf node — a node with no children. Then it backtracks back to the root node and follows the next branch down from there.

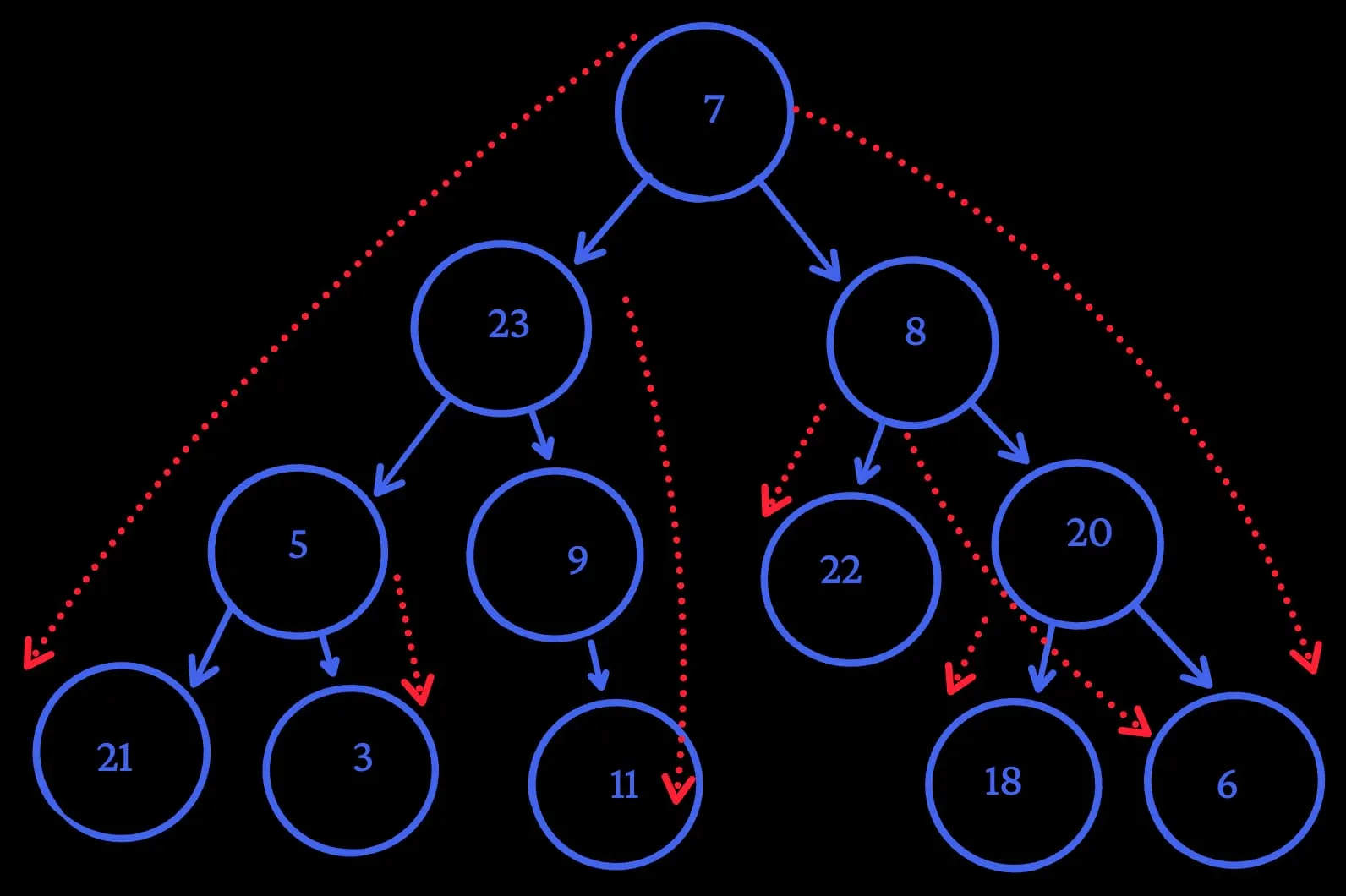
Breadth First Search

Breath first search, conversely, checks nodes on the same depth — hence, breadth, not depth. It starts at the root node, then traverses all children one level down, then moves on to the next level and traverses all children two levels down, so on and so forth.

Implementation

This can vary greatly, but for a rough overview, we can consider:

• Implementing DFS with a stack — last in first out. Traversing all nodes of the tree as we discover them. Read a node, put it’s children in the stack and read them as we discover them. Can use a recursive implementation.
• Implementing BFS with a queue — first in, first out. Add items to the queue as we discover them, then traverse them later when we enter that depth.

BFS

from collections import deque

def bfs(graph, start):
    visited = set()
    queue = deque([start])

    while queue:
        # Get first item in queue
        vertex = queue.popleft()
        if vertex not in visited:
            visited.add(vertex)
            print(f"{vertex} ")

            # Add neighbors of the vertex to the queue
            queue.extend(node for node in graph[vertex] if node not in visited)

# Example usage
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}
bfs(graph, 'A')

Note:

• The nodes get visited in the order they are added to the queue.
• All the current nodes in the queue get visited BEFORE the newly added nodes.

DFS

def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()

    visited.add(start)
    print(f"{start} ")

    for next_node in graph[start]:
        if next_node not in visited:
            dfs(graph, next_node, visited)

# Example usage
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}
dfs(graph, 'A')

Note:

• Recursion 🌪️
• All child + grandchild nodes of the current node get visited before moving on to traversing all nodes of another node.
• For this reason, D gets visited before C.

Comparison

• En corto: bfs = visit neighbors first; dfs = visit children first.
• Depth first search preserves shape, whereas breadth first search does not.
• BFS is generally better for shortest path algorithms.
• DFS is generally better when the solution is expected to be found far from the root node or in scenarios where the tree is very deep and solutions are rare.
• In infinite graphs, DFS might be a better, more efficient way to a solution. If the graph has deep recursive paths, BFS could be a better option.
• DFS might be more straightforward in undirected graphs or cycle detection in directed graphs.