The “Computation Graph”

Videos:

• Computation Graph
• Derivatives with Computation Graph

We use the term “Computation graph” to refer to basically the sequence and layout of interconnected functions in a neural network. Again, this is a graph in the data structure sense, not a pictoral. Each node in the graph is a function.

Here’s a basic representation of a computation graph.

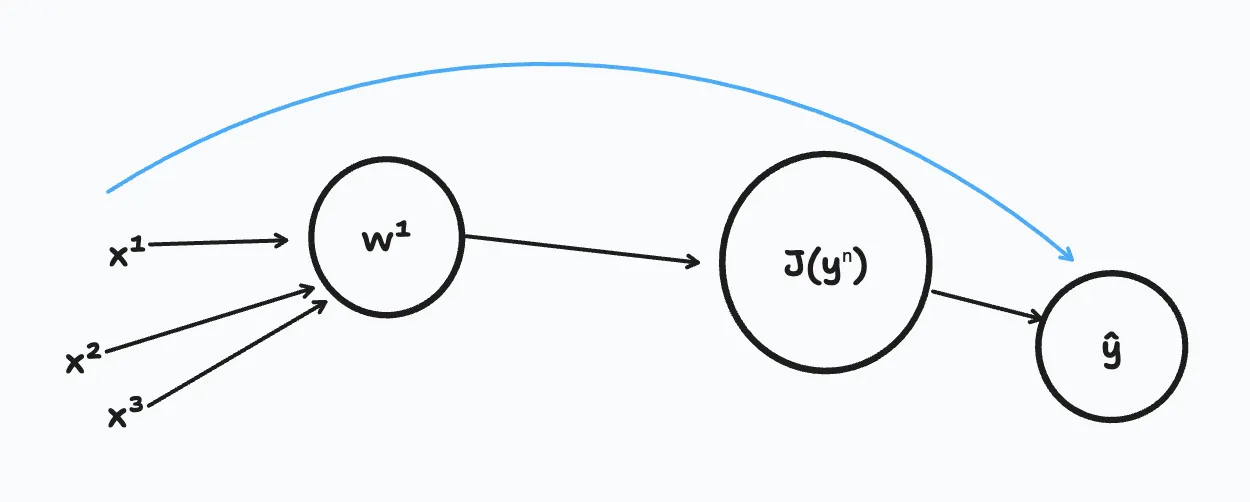
As we know, J is the loss function. As we move left to right (the blue arrow), we can calculate J. In the case of logistic regression, J is the cost function that we’re trying to minimize.

In order to compute derivatives, we need to go right to left (the red arrow).

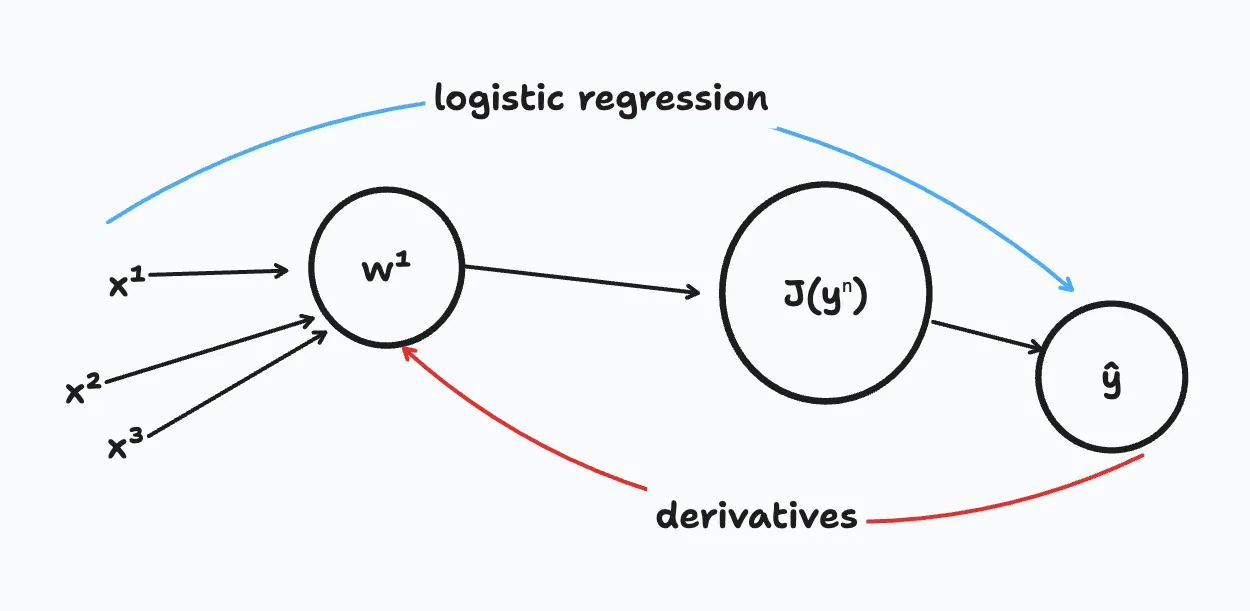
This is important to understanding backpropagation.

Calculus Chain Rule

In calculus, there’s a concept relating to computation graphs and derivatives called the chain rule. We can rely on the chain rule to calculate derivatives for situations in which we have more than one function at play in our computation graph. This rule basically states that:

• if we have a function, like: y = f(g(x))
• and if y = f(u) and u = g(x)
• then dy/dx = df/du * du/dx is true. d here meaning derivatives.

So, if we know the derivatives of the functions f and g, we can use the chain rule to find the derivative of their composition y = f(g(x)) with respect to x.

Related To Backpropagation

Computation graphs are important concepts in deep learning for training neural networks.

TODO: how?