Derivatives

Videos:

• Derivatives

This is basically a slapdash overview of the basic calculus behind deep learning. We don’t need to become experts on calculus, but we do need to understand some stuff. We can also basically consider this a one-n-done implementation — the calculus involved is usually tucked away into reusable abstractions.

Intuition about Derivatives

“Derivatives” in down-to-earth language can be understood as a slope. Like in a plot on a chart, the incline.

Given a certain slope on a chart, the derivative is the same, regardless of where you are.

Say for example, we have a function f(a) = 3a. Regardless of if the input is 6 or 15, the difference between 6 -> 6.001 and 15 -> 15.001 is the same, 3.

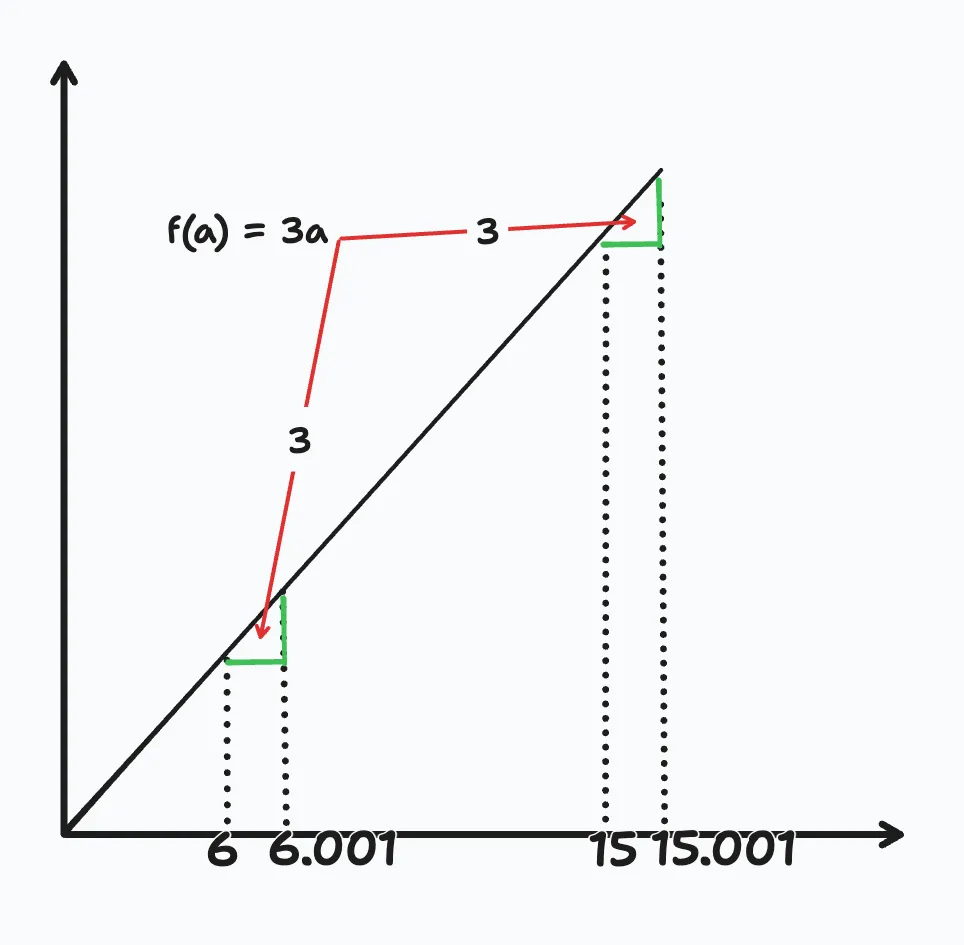
The green section shows the derivative, the same at 6 and 15.

Our equation f(a) = 3a is simply the slope that defines the graph. In this example, the derivative is always equal to 3 since it’s just a linear function.

Not all functions are linear, though.

What if our graph is more complex? What if our slope is not just a simple straight line, but something exponential?

Consider a more complex example, e.g., f(a) = a².

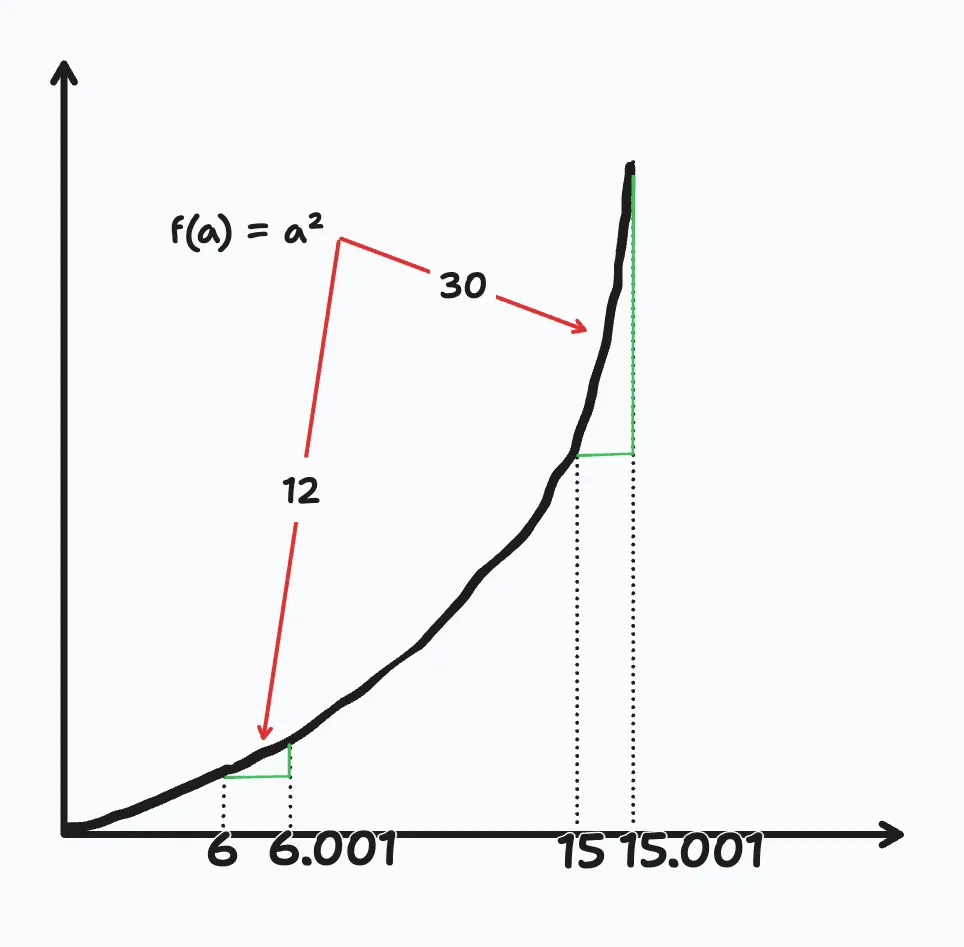
In this example, our derivative is f(a) = 2x. That is, at any point on the graph, we can calculate the derivative by multiplying the point by 2.

So, as we can see, as we go up the slope, the value of the change between two values is not the same. At 6, the value of the derivative is 12, at 15 the value is 30.

Simply Put

In very simple terms, the derivative is a representation of the rate of change of a function with respect to its input variable.