Bezier Curves

Bezier Curves are parametric curves defined by control points.

These were named after Pierre Bézier, a French engineer working at Renault in the 1960s who popularized their use for defining smooth mathematically-defined curves when designing cars.

But! These are also extremely widely used in computer graphics and font design due to their smoothness and versatility and control. Basically think of the pen tool in Adobe Illustrator.

When it comes to fonts, typography, and type design, font rendering relies heavily on bezier curves to define glyph outlines.

Types of Bezier Curves

Note: in the pseudocode implementation of the algorithms, t is a value between 0 and 1. Iterate t to compute points along the curve. For example, loop over t = 0 to t = 1 with small steps (e.g., 0.01) to draw or visualize the curve. The bezier function returns the x,y coordinates of the point t along the curve.

1. Quadratic Bezier Curves

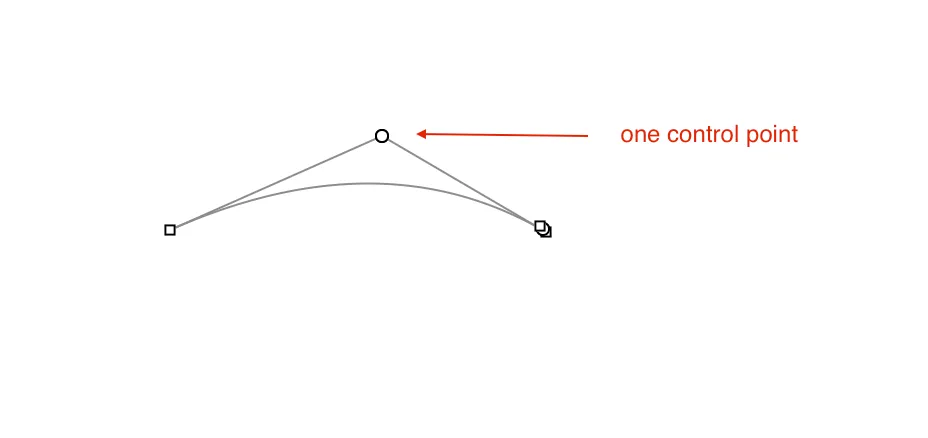
• Defined by 3 points: start (P0), control (P1), and end (P2).
• Simple and efficient, used in systems like TrueType fonts.
• The curve is interpolated using this algorithm:

function quadraticBezier(P0, P1, P2, t):
    x = (1 - t)^2 * P0.x + 2 * (1 - t) * t * P1.x + t^2 * P2.x
    y = (1 - t)^2 * P0.y + 2 * (1 - t) * t * P1.y + t^2 * P2.y
    return (x, y)

2. Cubic Bezier Curves

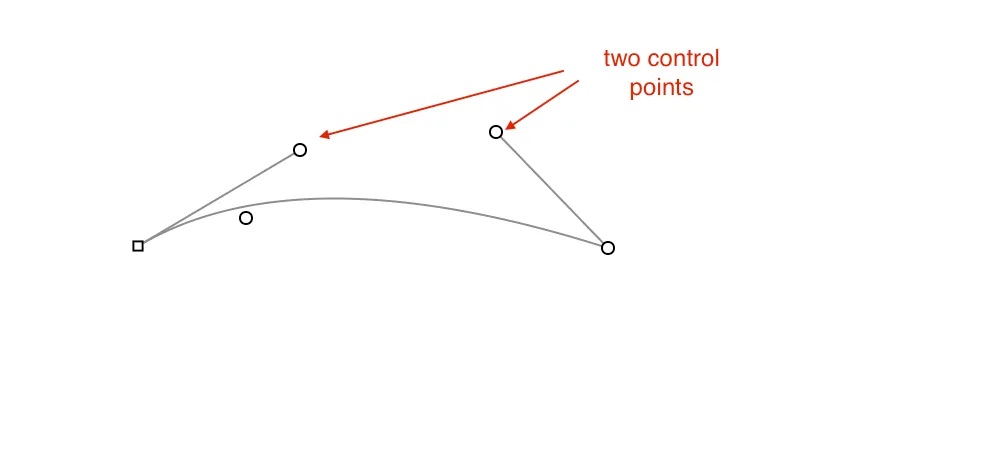
• Defined by 4 points: start (P0), 2 control points (P1, P2), and end (P3).
• More flexible, used in PostScript (OpenType) and SVG for precise shapes.
• The curve is interpolated using this algorithm:

function cubicBezier(P0, P1, P2, P3, t):
    x = (1 - t)^3 * P0.x + 3 * (1 - t)^2 * t * P1.x + 3 * (1 - t) * t^2 * P2.x + t^3 * P3.x
    y = (1 - t)^3 * P0.y + 3 * (1 - t)^2 * t * P1.y + 3 * (1 - t) * t^2 * P2.y + t^3 * P3.y
    return (x, y)

Further resources:

• This Video
• A Primer on Bézier Curves